⏪ Blaenorol Nesaf ⏩


Mae’r tri agwedd ymarferion codio da, Dogfennaeth, Modiwlareiddio, a Phrofion Awtomatig, yn gweithio’n gwell gyda’i gilydd. Nid yw’n gwneud synnwyr gofyn pa un fydd orau i’w wneud.

Mae’r ddelwedd isod yn dangos y perthynas rhwng y tri pheth:

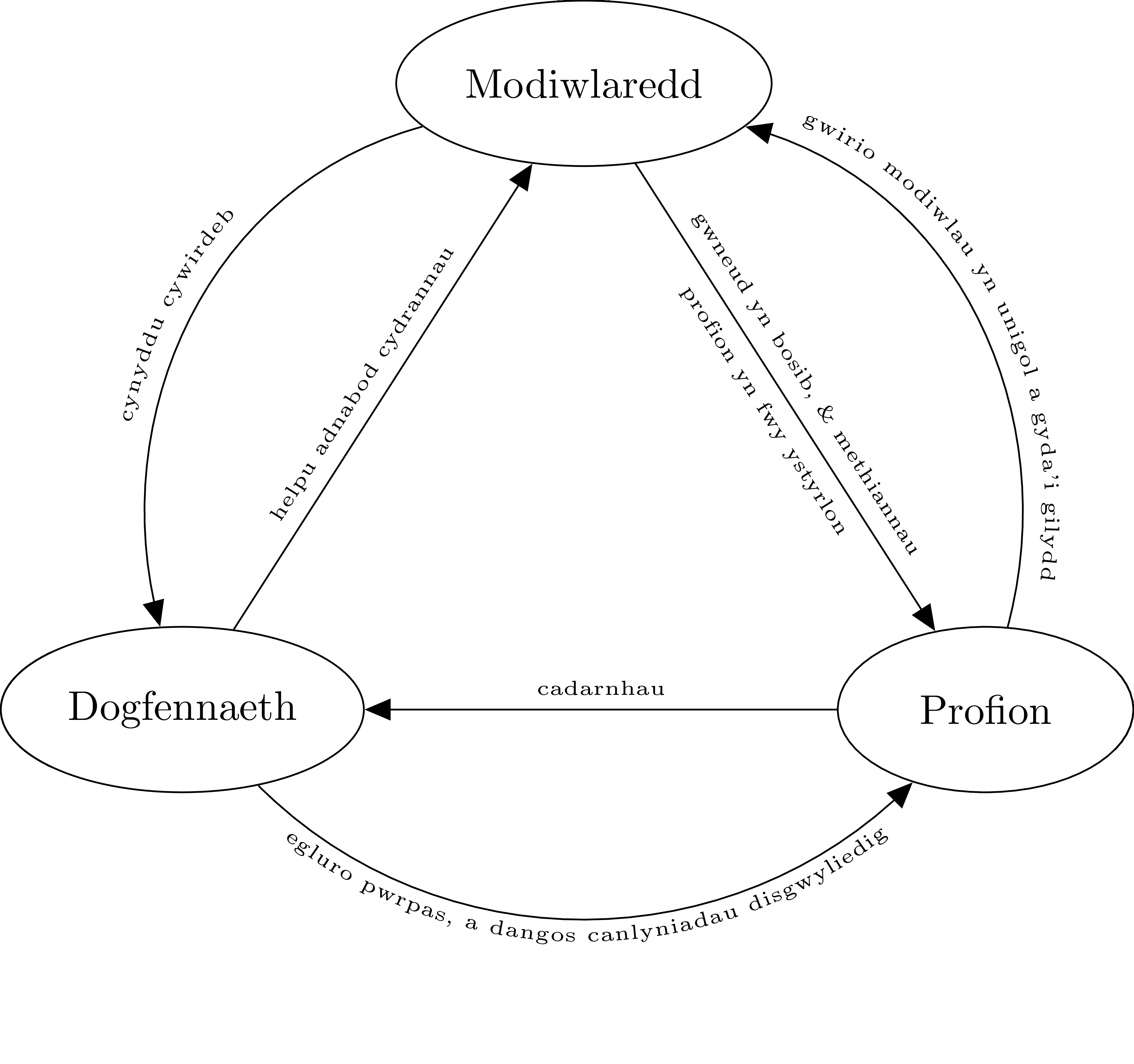
  • Dogfennaeth & Modiwlaredd: Mae cod darllenadwy yn helpu adnabod lle allwn torri lan y cod. Ac mae cydrannau bach yn cynyddu cywirdeb y ddogfennaeth. Mae enwau ffwythiannau yn bwysig iawn: os na allwn feddwl am enw ystyrlon cryno ar gyfer beth mae ffwythiant yn gwneud, fel arfer arwydd yw hwn gallwn dorri’r ffwythiant lan ymhellach.
  • Dogfennaeth & Profion: Mae dogfennaeth a phrofion yn helpu egluro pwrpas cod. Mae dogfennaeth felly yn egluro pwrpas y profion, ac mae profion felly yn cadarnhau beth ddywedir yn y ddogfennaeth. Os nad yw’r rhain yn cytuno, nid yn unig yw’r cod yn anodd ei ddarllen a deall, ond ni all y cod cyflawni beth y ddisgwylir.
  • Modiwlaredd & Profion: Mae torri lan y cod yn gwneud hi’n bosibl i brofi’r cod, gan fod angen ffwythiannau, gwrthrychau a modiwlau i fedru rhedeg profion. Mae profion yn sicrhau bod y cydrannau yma yn gweithio fel y disgwylir, ar wahân a gyda’i gilydd. Hefyd mae profi darnau bach o god yn cynyddu ystyr y negeseuon gwallau, trwy adnabod yn union ble yn y cod mae gwall, a beth yn union sydd o’i le.

Fel adolygiad o’r adran yma, ystyriwn enghraifft o godio Algorithm Euclid ar gyfer canfod ffactor cyffredin mwyaf dau rif.

Mae’r cais cyntaf y gweithredu’r algorithm:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

a = 1071
b = 462
C = []

while a != 0 and b != 0: i=0
    while a >= b:
        a -= b
        i += 1
    a, b = b, a
    C.append(i)
C.append(a)
C.append(b)

print(max(C))

Serch hynny, mae’n anodd iawn i’w ddarllen os nad ydyn yn gwybod Algorithm Euclid (N.B. does dim angen gwybod Algorithm Euclid; dylai cod da bod yn hunan esboniadol).

Ychwanegwn ddogfennaeth:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

mwyaf = 1071
lleiaf = 462
ffactorau = []

# Algorithm Euclid
while mwyaf != 0 and lleiaf != 0:
    lluosrif = 0
    while mwyaf >= lleiaf:
        mwyaf -= lleiaf
        lluosrif += 1
    mwyaf, lleiaf = lleiaf, mwyaf # cyfnewid enwau'r newidynnau
    ffactorau.append(lluosrif)
ffactorau.append(mwyaf)
ffactorau.append(lleiaf)

print(max(ffactorau))

Mae hwn bach mwy darllenadwy, ond mae’n edrych fel bloc mawr o god.

Torrwn ni’r cod i fyny. Mae lŵp o fewn lŵp, felly mae’n gwneud synnwyr tynnu un lŵp mas fel ffwythiant:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def tynnu_lluosrifau(mwyaf, lleiaf):
    """
    Faint o weithiau mae un rhif yn mynd mewn i rhif arall
    """
    lluosrif = 0
    while mwyaf >= lleiaf:
        mwyaf -= lleiaf
        lluosrif += 1
    return mwyaf, lleiaf, lluosrif

def ffactor_cyffredin_mwyaf(mwyaf, lleiaf):
    """
    Algorithm Euclid y canfod ffactor mwyaf cyffredin dau rhif
    """
    ffactorau = []
    while mwyaf != 0 and lleiaf != 0:
        lleiaf, mwyaf, lluosrif = tynnu_lluosrifau(mwyaf, lleiaf)
        ffactorau.append(lluosrif)
    ffactorau.append(mwyaf)
    ffactorau.append(lleiaf)
    return max(ffactorau)

print(ffactor_cyffredin_mwyaf(1071, 462))

Nid yw enw’r ffwythiant cyntaf, tynnu_lluosrifau yn gwneud lot o synnwyr. Mae’n anodd iawn disgrifio beth sy’n mynd ymlaen fan hyn, felly efallai mai modd torri’r cod lawr rhagor.

  • Beth mae’r cod yn ei wneud?
    • Rhoi faint o weithiau mae lleiaf yn mynd mewn i mwyaf,
    • Rhoi lleiaf nol,
    • Rhoi gweddill ar ôl tynnu lleiaf o mwyaf gymaint o weithiau a gallwn.

Mae hwn wedi uwcholeuo ffordd o wella’r ffwythiant hynny (mewn gwirionedd does dim angen ffwythiant arall ar gyfer y gweithrediad yma, mae datganiad % Python yn gwneud y job. Cofiwch y rheol ‘paid ailddyfeisio’r olwyn’, os oes cod sy’n gwneud y job yn barod, defnyddia hi!):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

def ffactor_cyffredin_mwyaf(mwyaf, lleiaf):
    """
    Algorithm Euclid y canfod ffactor mwyaf cyffredin dau rhif
    """
    ffactorau = []
    while mwyaf != 0 and lleiaf != 0:
        gweddill = mwyaf % lleiaf
        lluosrif = (mwyaf - gweddill) / lleiaf
        mwyaf = lleiaf
        lleiaf = gweddill
        ffactorau.append(lluosrif)
    ffactorau.append(mwyaf)
    ffactorau.append(lleiaf)
    return max(ffactorau)

print(ffactor_cyffredin_mwyaf(1071, 462))

Nawr bod gennym god cryno, darllenadwy, a modwlar (wel ond un ffwythiant oedd angen yn yr achos yma), ysgrifennwn brofion i sicrhau bod hwn yn gweithio fel y disgwylir:

1
2
3
4
5

assert ffactor_cyffredin_mwyaf(1071, 462) == 21
assert ffactor_cyffredin_mwyaf(20, 4) == 5
assert ffactor_cyffredin_mwyaf(101, 60) == 6
assert ffactor_cyffredin_mwyaf(81, 82) == 81
assert ffactor_cyffredin_mwyaf(10, 8) == 4

Ac felly mae gennym ffwythiant y gellir ei ailddefnyddio, wedi ysgrifennu mewn ffordd ddarllenadwy a dealladwy, wedi’i phrofi ar gyfer nifer o achosion.

Cyfeiriadau

⏪ Blaenorol Nesaf ⏩